术语解释

在介绍排序算法前，有必要讲一下什么是稳定排序、原地排序、时间复杂度、空间复杂度：

• 稳定排序：如果 a 原本在 b 的前面，且 a == b，排序之后 a 仍然在 b 的前面，则为稳定排序。
• 非稳定排序：如果 a 原本在 b 的前面，且 a == b，排序之后 a 可能不在 b 的前面，则为非稳定排序。
• 原地排序：原地排序就是指在排序过程中不申请多余的存储空间，只利用原来存储待排数据的存储空间进行比较和交换的数据排序。
• 非原地排序：需要利用额外的数组来辅助排序。
• 时间复杂度：一个算法执行所消耗的时间，也即对排序数据的总的操作次数，反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，反映运行完一个算法所需的内存大小，它也是数据规模n的函数。

十大排序算法

十种常见排序算法可以分为两大类：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。

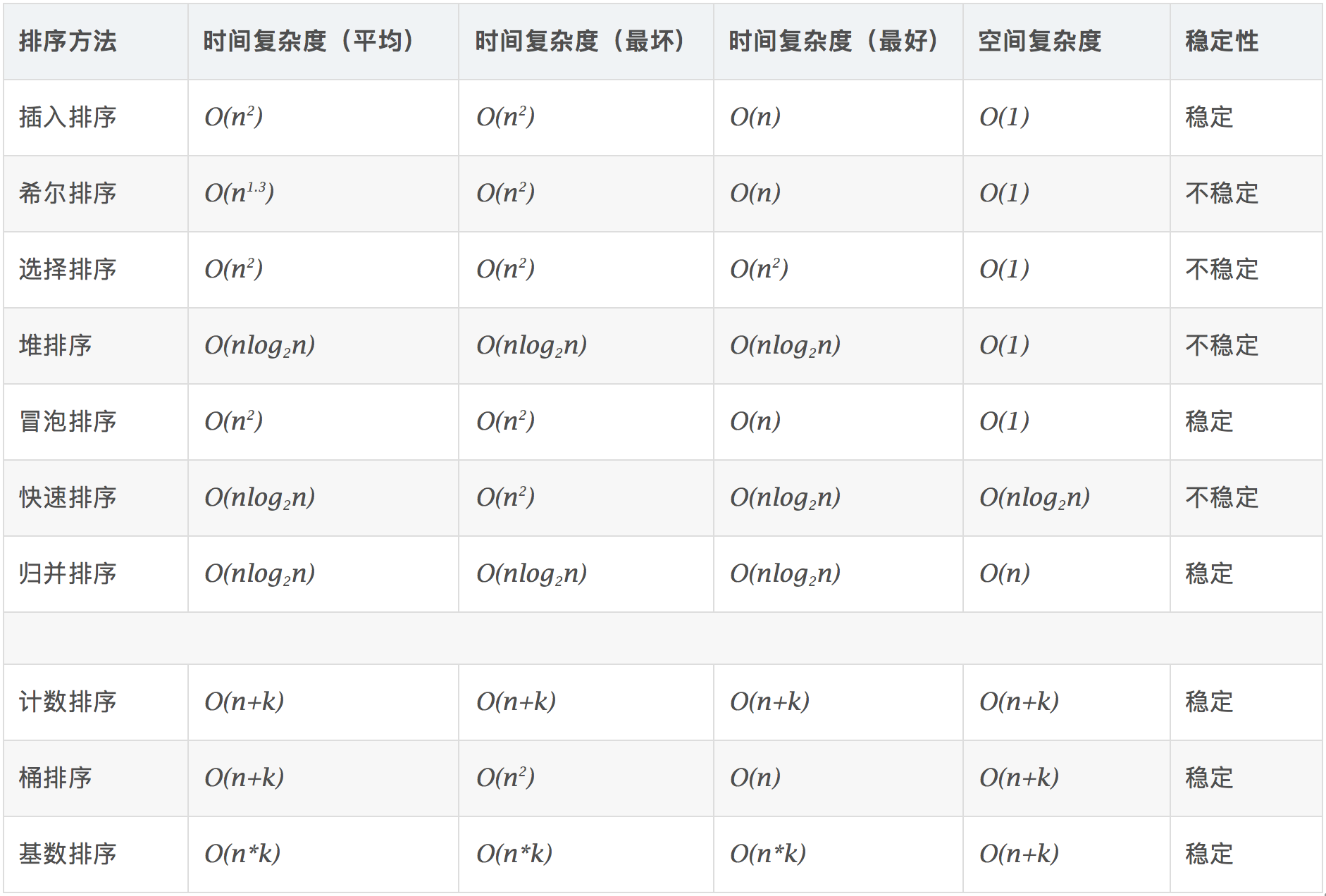
各个算法的复杂度如下所示：

插入排序 Insertion Sort

插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。 比如，在玩打牌时，该如何整理那些牌呢？一种简单的方法就是一张一张来，将每一张牌插入到其他已经有序的牌中的适当位置。 当我们给无序数组做排序的时候，为了要插入元素，我们需要腾出空间，将其余所有元素在插入之前都向右移动一位，这种算法我们称之为插入排序。

算法描述

一般来说，插入排序都采用in-place在数组上实现。具体算法描述如下：

1. 从第一个元素开始，该元素可以认为已经被排序；
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描；
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置；
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；
5. 将新元素插入到该位置后；
6. 重复步骤2~5。

算法演示

代码实现

算法分析

选择排序

冒泡排序

快速排序

堆排序

基数排序

归并排序

计数排序

希尔排序

桶排序

Comments

Be the first one to comment on this page!